# 排序算法
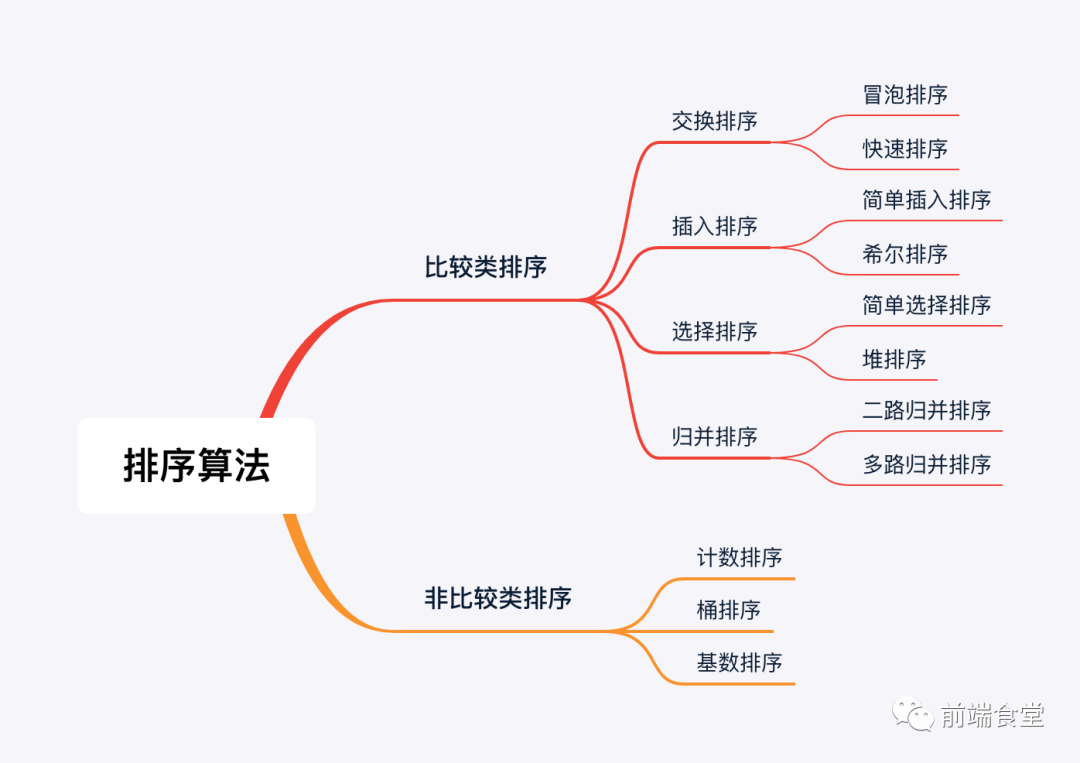
排序算法分类
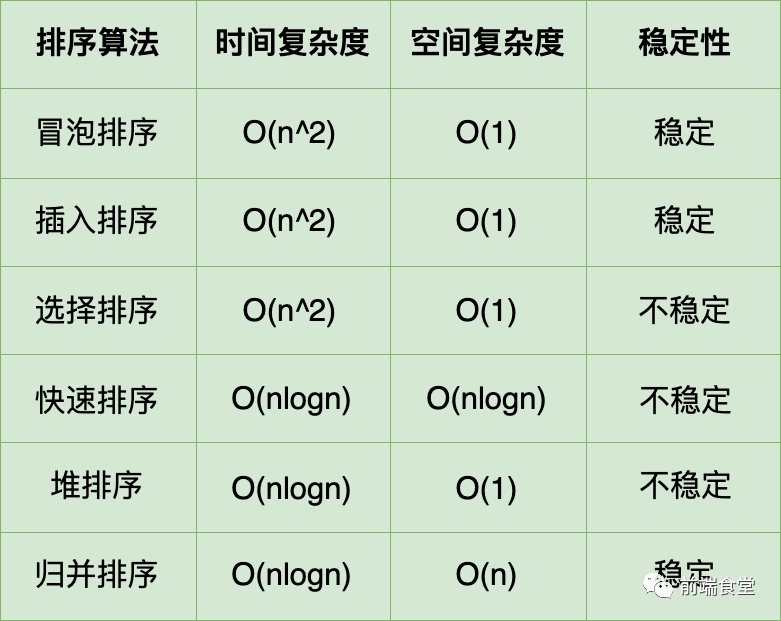
算法复杂度
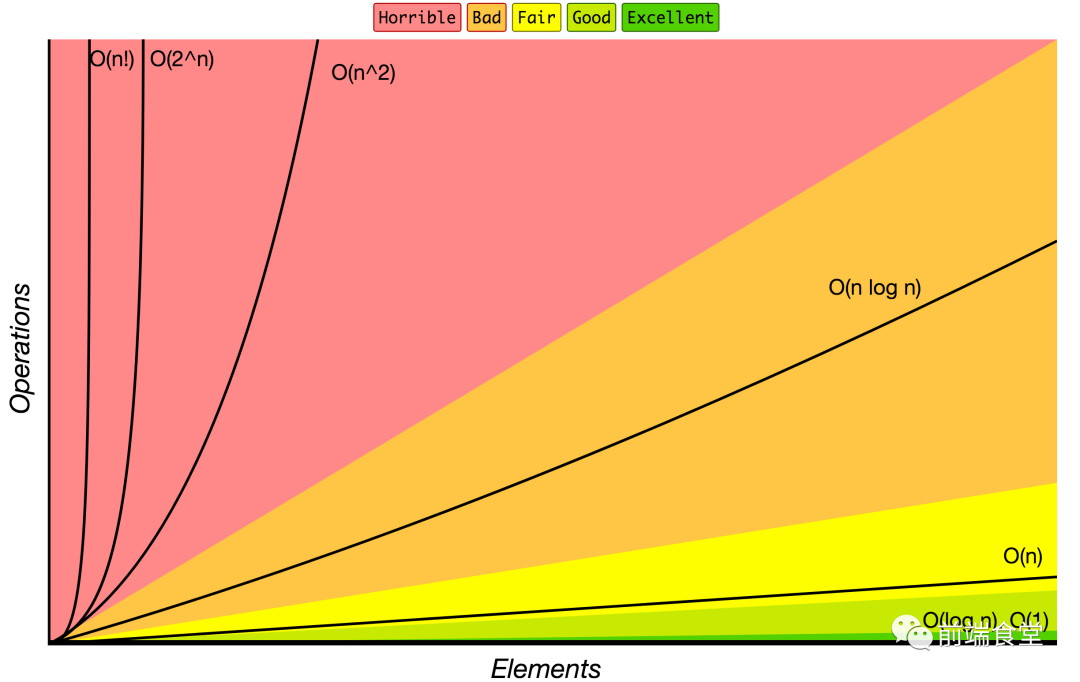
基础数据
var arr = [773, 377, 772, 79, 209, 578, 706, 434, 667, 315, 449, 892, 894, 839, 757, 987, 37, 182, 22, 188]
# 冒泡排序
基础思想:冒泡排序在每次冒泡操作时会比较相邻的两个元素,看是否满足大小关系要求,不满足就将它俩互换。一直迭代到不再需要交换,也就是排序完成
时间复杂度:O(n^2)
空间复杂度:O(1)
稳定性:稳定
function bobbleSort(arr) {
const len = arr.length
let flag = false
if(len < 2) return arr;
for(var i = 0; i < len - 1; i++) {
flag = false
for(var j = 0; j < len - i - 1; j++) { // 每次大循环就找到一个数,所以减去 i
if(arr[j] > arr[j + 1]) { // 判断相邻两个那个大
var max = arr[j]
arr[j] = arr[j+1]
arr[j + 1] = max
flag = true
}
}
if(!flag) break;
}
}
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
# 插入排序
基础思想:从后往前扫描数组,找到相应的位置进行插入,保持已排序序列中元素一直有序。
时间复杂度: O(n^2)
空间复杂度:O(1)
稳定性: 稳定
function insertSort(arr) {
const len = arr.length;
let curr;
let prev;
for(var i = 0 ; i < len ; i++) {
curr = arr[i]; // 当前项
prev = i - 1; // 上一项的下标
while(prev >= 0 && arr[prev] > curr) { // 如果前面的数大于当前项,进行交互,升序
arr[prev + 1] = arr[prev]
prev --
}
arr[prev + 1] = curr
}
}
2
3
4
5
6
7
8
9
10
11
12
13
14
15
# 选择排序
基础思想:将最小的元素存放在数组起始位置,再从剩下的未排序的序列中寻找最小的元素,然后将其放到已排序的序列后面
时间复杂度:O(n^2)
空间复杂度:O(1)
稳定性:不稳定
function selectionSort(arr) {
const len = arr.length;
let temp, minIndex
for(var i = 0; i < len; i++) {
minIndex = i
for(j = i + 1; j < len; j++) {
if(arr[j] <= arr[minIndex]) {
minIndex = j //
}
}
temp = arr[i]
arr[i] = arr[minIndex]
arr[minIndex] = temp
}
}
selectionSort(arr)
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
# 归并排序
基础思想:先处理子问题,然后再合并。
- 分解:将原问题分解成一系列子问题。
- 解决:递归求解各个子问题,若子问题足够小,则直接求解。
- 合并:将子问题的结果合并成原问题。
时间复杂度:O(nlogn)
空间复杂度:O(n)
稳定性:稳定
const mergeSort = function(arr) {
const merge = (right, left) => {
const result = []
let i = 0, j = 0
while (i < left.length && j < right.length) {
if (left[i] < right[j]) {
result.push(left[i++])
} else {
result.push(right[j++])
}
}
while (i < left.length) {
result.push(left[i++])
}
while (j < right.length) {
result.push(right[j++])
}
return result
}
const sort = (arr) => {
if (arr.length === 1) { return arr }
const mid = Math.floor(arr.length / 2)
const left = arr.slice(0, mid)
const right = arr.slice(mid, arr.length)
return merge(mergeSort(left), mergeSort(right))
}
return sort(arr)
}
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
# 快速排序
基础思想:快速排序也是分治法的应用。从数组中挑选出一个元素作为 基准(pivot),然后重新排序数列,将元素比基准值小的放到基准前面,比基准值大的放到基准后面。然后将小于基准值的子数组(left)和大于基准值的子数组(right)递归地调用排序,直到排序完成。
时间复杂度: O(nlogn)
空间复杂度:O(nlogn)
稳定性:不稳定
const quickSort = function(arr) {
const quick = function(arr) {
if (arr.length <= 1) return arr
const len = arr.length
const index = Math.floor(len >> 1)
const pivot = arr.splice(index, 1)[0]
const left = []
const right = []
for (let i = 0; i < len; i++) {
if (arr[i] > pivot) {
right.push(arr[i])
} else if (arr[i] <= pivot) {
left.push(arr[i])
}
}
return quick(left).concat([pivot], quick(right))
}
const result = quick(arr)
return result
}
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
# 堆排序
# 前置知识
堆是一种特殊的树,满足以下两点就是堆:
- 堆是一个完全二叉树
- 堆中每一个节点的值都必须大于等于(或小于等于)其子树中的每个节点的值
每个节点的值都大于等于子树中每个节点值的堆,叫做大顶堆,每个节点的值都小于等于子树中每个节点值的堆,叫做小顶堆。也就是说,大顶堆中,根节点是堆中最大的元素。小顶堆中,根节点是堆中最小的元素。
TIP
堆如果用一个数组表示的话,给定一个节点的下标 i (i从1开始),那么它的父节点一定为 A[i / 2],左子节点为 A[2i],右子节点为 A[2i + 1]。
基础思想:将数据建立成一个堆结构,然后将堆排序。
TIP
堆排序包含两个过程,建堆和排序。
首先构建一个大顶堆,也就是将最大值存储在根节点(i = 1)。
每次取大顶堆的根节点与堆的最后一个节点进行交换,此时最大值放入了有效序列的最后一位,并且有效序列减 1,有效堆依然保持完全二叉树的结构,然后进行堆化成为新的大顶堆。
重复此操作,直到有效堆的长度为 0,排序完成。
时间复杂度:O(nlogn)
空间复杂度:空间复杂度: O(1)
稳定性:不稳定
# 快速排序 Quick Sort
基础思想:
时间复杂度:
空间复杂度:
稳定性:
# 快速排序 Quick Sort
# 参考
时间复杂度:
空间复杂度:
稳定性:
``` -->