图解算法

第一章 算法简介

1.1引言

• 对数，log 32表示以2为底，32的对数，也就是 几个2相乘是32

1.1.1性能方面

1.2二分查找

• 必须是有序列表
• 时间复杂度O(log n)

var arr = [1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16,17]
var first = 0
var last = arr.length -1
var target = 17
while(first < last) {
  var mid = parseInt((first + last)/2 ) // 7
  var current = arr[mid] // 8
  if(target < current) {
    last = mid - 1
  } else if(target > current) {
    first = mid + 1
  }
  else{
    console.log(`第${mid}位的数字是${target}`)
    break;
  }
}

1.3大O表示法

• 大O表示法指的并非以秒为单位的速度。大O表示法让你能够比较操作数，它指出了算法运行时间的增速。

1.3.4 一些常见的大 O 运行时间

• O(log n)，也叫对数时间，这样的算法包括二分查找。
• O(n)，也叫线性时间，这样的算法包括简单查找。
• O(n * log n)，这样的算法包括第4章将介绍的快速排序——一种速度较快的排序算法,最糟糕是 O(n^2)。 合并排序时间复杂度 (n * log n)
• O(n2)，这样的算法包括第2章将介绍的选择排序——一种速度较慢的排序算法。
• O(n!)，这样的算法包括接下来将介绍的旅行商问题的解决方案——一种非常慢的算法。

第二章 选择排序

2.1 内存的工作原理

需要将数据存储到内存时，你请求计算机提供存储空间，计算机给你一个存储地址。需要存 储多项数据时，有两种基本方式——数组和链表。

2.2 数组和链表

链表

1. 分散内存分配
2. 插入 时间负责度 O(log 1)
3. 查找 时间负责度 O(log n)
4. 删除 时间复杂度 O(log 1)

数组

1. 连续的内存分配
2. 插入 时间负责度 O(log n)
3. 查找 时间负责度 O(log 1)
4. 删除 时间复杂度 O(log n)

2.3 选择排序

1. 时间复杂度 O(log n^2)

小结

1. 中间插入用链表
2. 删除也用链表

第三章 递归

1. 递归只是让方案更优雅，并没有性能上的优势
2. 有时循环性能会更好

3.2 基线条件和递归条件

1. 基线条件就是啥时候不再调用自己
2. 递归条件就是函数调用自己

3.3 调用栈

计算机在内部使用被称为调用栈的栈。

function factorial(num) {
  if(num <= 1) {
    return 1
  }
  return num * factorial(num -1)

}
var count = factorial(6)

小结

 递归指的是调用自己的函数。  每个递归函数都有两个条件：基线条件和递归条件。  栈有两种操作：压入和弹出。  所有函数调用都进入调用栈。  调用栈可能很长，这将占用大量的内存。

第四章 快速排序

快速排序是一种排序算法，速度比第2章介绍的选择排序快得多，实属优雅代码的典范。

4.1 分而治之 （divide and conquer，D&C）

下D&C的工作原理：

1. 找出简单的基线条件；
2. 确定如何缩小问题的规模，使其符合基线条件。

::: tips 编写涉及数组的递归函数时，基线条件通常是数组为空或只包含一个元素。陷入困境时， 请检查基线条件是不是这样的。 :::

4.2 快速排序

快速排序是一种常用的排序算法，比选择排序快得多，选择基数，最好选择中间元素

function quickSort(arr) {
  if(arr.length < 2) {
    return arr
  }
  var pivot = arr[0]
  var less = []
  var greater =  []
  arr.slice(1).forEach(item => {
    if(item <= pivot){
      less.push(item)
    } else if(item > pivot){
      greater.push(item)
    }
  })
  return quickSort(less).concat( pivot,quickSort(greater))
}
var arr = [94,5,62,3,4,345,23324,32,63,2,94,5,62,3,4,345,23324,32,63,2,94,5,62,3,4,345,23324,32,63,2]
var count = quickSort(arr)
console.log('count', count)

第五章 散列表

最有用的基本数据结构之一

内部机制：实现、冲突和散列函数

js中的对象

5.1 散列函数( hash table)也被称为散列映射、映射、字典和关联数组

散列函数“将输入映射到数字

散列函数( hash table)也被称为散列映射、映射、字典和关联数组

要求

1. 它必须是一致的
2. 它应将不同的输入映射到不同的数字

特点

1. 散列函数总是将同样的输入映射到相同的索引
2. 散列函数将不同的输入映射到不同的索引
3. 散列函数知道数组有多大

大O表示法

1. 查找 O(1)
2. 插入 O(1)
3. 删除 O(1)

应用

1. 电话本查找
2. DNS解析
3. Redis 数据库

第6章 广度优先搜索 （breadth-first search，BFS）

解决最短路径问题的算法被称为广度优先搜索。

1. 使用新的数据结构图来建立网络模型。
2. 学习广度优先搜索，可以回答 “到X的最短路径是什么“
3. 学习有向图和无向图
4. 学习拓扑排序，这种排序算法指出了节点之间的依赖关系。
5. 时间复杂度为O(V + E)

如果你在你的整个人际关系网中搜索芒果销售商，就意味着你将沿每条边前行（记住，边是 从一个人到另一个人的箭头或连接），因此运行时间至少为O(边数)。 你还使用了一个队列，其中包含要检查的每个人。将一个人添加到队列需要的时间是固定的， 即为O(1)，因此对每个人都这样做需要的总时间为O(人数)。所以，广度优先搜索的运行时间为 O(人数 + 边数)，这通常写作O(V + E)，其中V为顶点（vertice）数，E为边数。

6.2 图是什么

图模拟一组连接,图由节点（node）和边（edge）组成。

一个节点可能与众多节点直接相连，这些节点被称为邻居。

6.3 广度优先搜索

广度优先搜索是一种用于图的查找算法，可帮助回答两类问题。

1. 从节点A出发，有前往节点B的路径吗？
2. 从节点A出发，前往节点B的哪条路径最短？

6.3.2 队列

特点：先进先出 First In First Out，FIFO（栈后进先出（Last In First Out，LIFO） 操作：入队和出队

6.4 实现图

有向图：有箭头指向的，有方向性的图

无向图：没有箭头指向的，没有方向的

树是一种特殊的图,其中没有往后指的边。

通过散列表（js中的对象）实现图

var graph = {} 
graph["you"] = ["alice", "bob", "claire"] 
graph["bob"] = ["anuj", "peggy"] 
graph["alice"] = ["peggy"] 
graph["claire"] = ["thom", "jonny"] 
graph["anuj"] = [] 
graph["peggy"] = [] 
graph["thom"] = [] 
graph["jonny"] = []

有没有某人

var tu = {
  曹: ['佳宇', '杨欣', '志凯'],
  佳宇: ['武阳', '妥强', '志凯'],
  志凯: ['王维'],
  杨欣:['王维'],
  王维: ['俊杰']
}
var searched = []
var searching = []
var tips = '没找到'
function search(name) {
  searching = tu[name]
  while(searching.length) {
    person = searching.shift()
    if (searched.indexOf(person) === -1) {
      searched.push(person)
      if(person === '俊杰') {
        tips = '找到了'
      }
      tu[person] && searching.push(...tu[person])
    }
  }

}
search('曹');

如果任务A依赖于任务B，在列表中任务A就必须在任务B后面。这被称为拓扑排序，使用它可根据图创建一个有序列表.

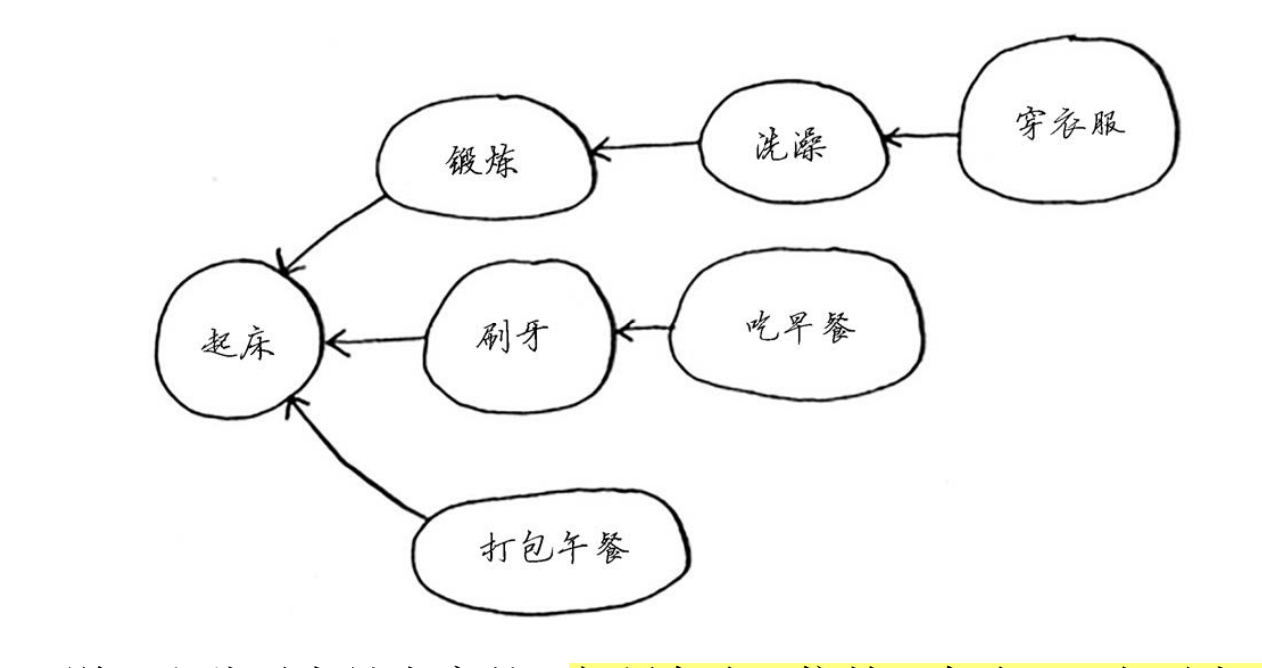
这是一个图，因为它由节点（人）和边组成。其中的边从一个节点指向其父母，但所有的边 都往下指。在家谱中，往上指的边不合情理！因为你父亲不可能是你祖父的父亲！

小结

•  广度优先搜索指出是否有从A到B的路径。
•  如果有，广度优先搜索将找出最短路径。
•  面临类似于寻找最短路径的问题时，可尝试使用图来建立模型，再使用广度优先搜索来 解决问题。
•  有向图中的边为箭头，箭头的方向指定了关系的方向，例如，rama→adit表示rama欠adit钱。
•  无向图中的边不带箭头，其中的关系是双向的，例如，ross - rachel表示“ross与rachel约 会，而rachel也与ross约会”。
•  队列是先进先出（FIFO）的。
•  栈是后进先出（LIFO）的。
•  你需要按加入顺序检查搜索列表中的人，否则找到的就不是最短路径，因此搜索列表必 须是队列。
•  对于检查过的人，务必不要再去检查，否则可能导致无限循环。

第7章 狄克斯特拉算法 （Dijkstra’s algorithm）

本章内容

1. 介绍加权图——提高或降低某些边的权重
2. 介绍狄克斯特拉算法，让你能够找出加权图中前往X的最短路径。
3. 介绍图中的环，它导致狄克斯特拉算法不管用。

广度优先搜索，它找出的是段数最少的路径（导航去某地 换乘少）。如果你要找出最快的路径，可使用另一种算法——狄克斯特拉 算法（Dijkstra’s algorithm）（导航去某地 用时少）。

DANGER

不能将狄克斯特拉算法用于包含负权边的图。在包含 负权边的图中，要找出最短路径，可使用另一种算法——贝尔曼福德算法（Bellman-Ford algorithm）

DANGER

在无向图中，每条边都是一个环。狄克斯特拉算法只适用于有向无环图（directed acyclic

graph，DAG）。

7.1 使用狄克斯特拉算法

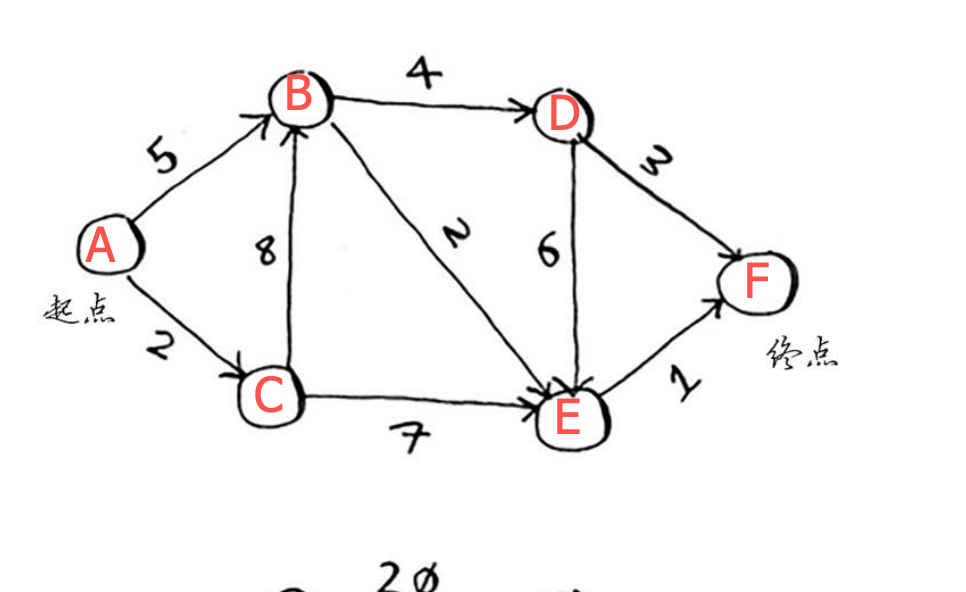
问题：找出下列图中，起点到终点耗时最少的路径。其中每个数字表示的都是时间，单位分钟

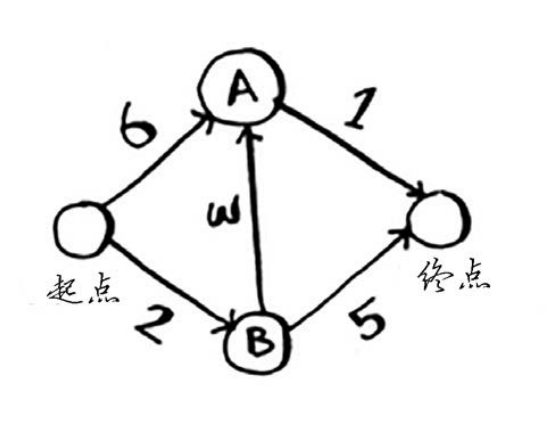
狄克斯特拉算法包含4个步骤。

1. 找出最便宜的节点，即可在最短时间内前往的节点。
2. 对于该节点的邻居，检查是否有前往它们的更短路径，如果有，就更新其开销。
3. 重复这个过程，直到对图中的每个节点都这样做了。
4. 计算最终路径。

求双子峰到金门大桥的最短时间

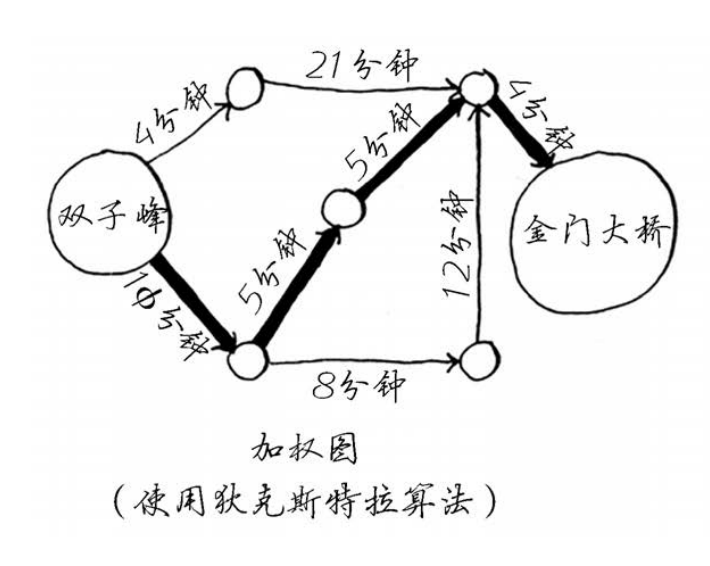
求双子峰到金门大桥的最短距离

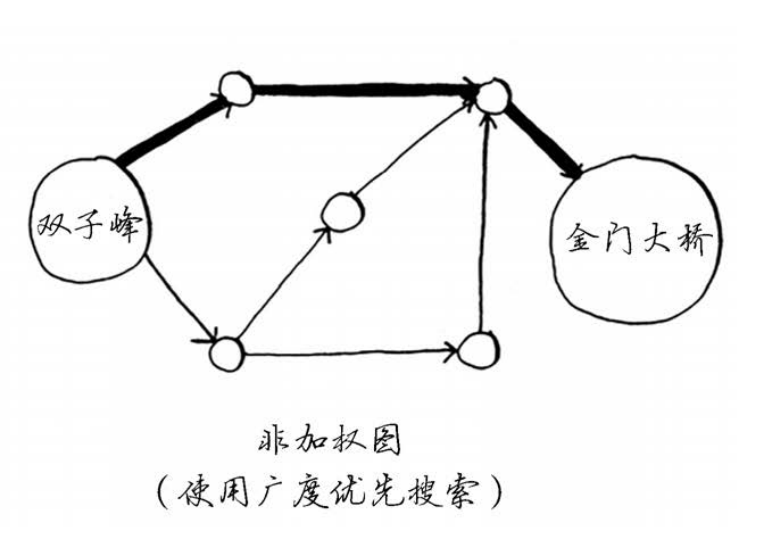
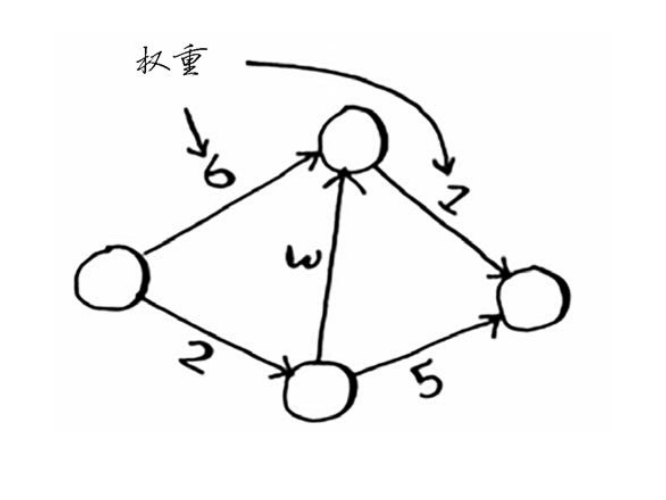
7.2 术语

狄克斯特拉算法用于每条边都有关联数字的图，这些数字称为权重（weight）。

带权重的图称为加权图（weighted graph），不带权重的图称为非加权图（unweighted graph）。

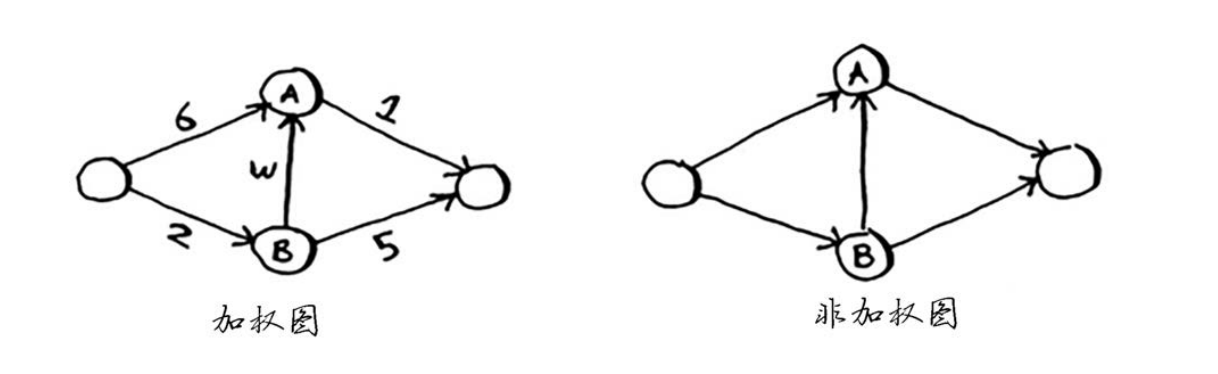
TIP

要计算非加权图中的最短路径，可使用广度优先搜索。要计算加权图中的最短路径，可使用狄克斯特拉算法

7.3 换钢琴

这个图中的节点是大家愿意拿出来交换的东西，边的权重是交换时需要额外加多少钱。拿海 报换吉他需要额外加30美元，拿黑胶唱片换吉他需要额外加15美元。Rama需要确定采用哪种路 径将乐谱换成钢琴时需要支付的额外费用最少。为此，可以使用狄克斯特拉算法！

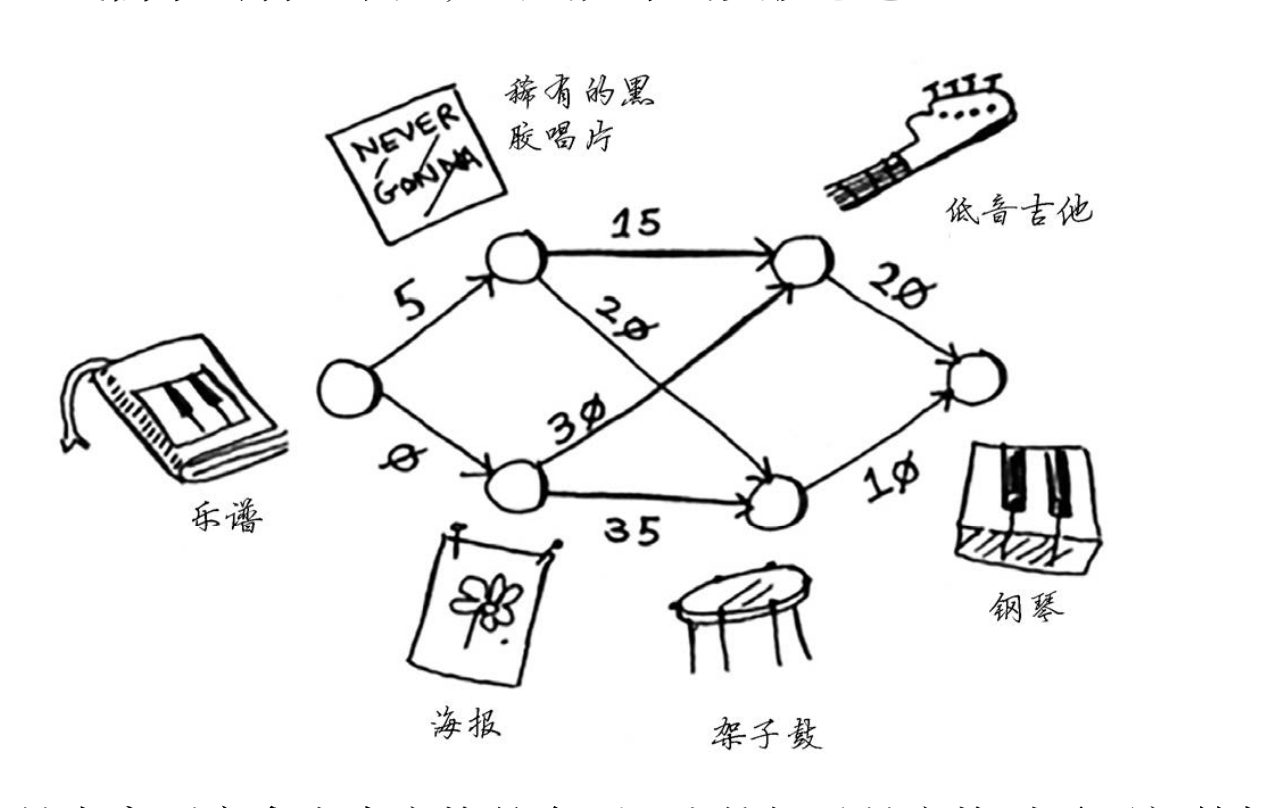
1. 由点【乐谱】出发，相邻【唱片】和【海报】两点，将它们放到开销数组中，值分别为 0 和 5。0 小于 5，所以基于【海报】，执行第二步，拿到【乐谱】通过【海报】达到其相邻的点的值，分别是【吉他】30 和【架子鼓】35，此时开销数组里面有四个值：

父节点	节点	开销
乐谱	海报	0 （已遍历相邻值）
乐谱	唱片	5
海报	吉他	30
海报	架子鼓	35

2. 5<30<35，进行重复操作，以【唱片】为基础，拿到【乐谱】到它相邻的点的值。分别为【吉他】20，【架子鼓】25，都小于开销数组中的值，进行更新。此时的开销数组为：

父节点	节点	开销
乐谱	海报	0 （已遍历相邻值）
乐谱	唱片	5 （已遍历相邻值）
唱片	吉他	20
唱片	架子鼓	25

3. 继续遍历，20 < 25，此时应该基于【吉他】，【吉他】与钢琴相连，【乐谱】通过【唱片】到【吉他】再到【钢琴】，需 40，更新数组。

父节点	节点	开销
乐谱	海报	0 （已遍历相邻值）
乐谱	唱片	5 （已遍历相邻值）
唱片	吉他	20（已遍历相邻值）
唱片	架子鼓	25
吉他	钢琴	40

4. 25 < 40，再基于【架子鼓】遍历，架子鼓也只和【钢琴】相连，【乐谱】——【唱片】——【架子鼓】——【钢琴】，值为 35，35 小于 40 ，更新。最终只有【钢琴】这一点没遍历，而【钢琴】又是终点，则执行结束啦。最终是：

父节点	节点	开销
乐谱	海报	0 （已遍历相邻值）
乐谱	唱片	5 （已遍历相邻值）
唱片	吉他	20（已遍历相邻值）
唱片	架子鼓	25 （已遍历相邻值）
架子鼓	钢琴	35 （终点，无需遍历）

5. 确定最终的路径。当前，我们知道最短路径的开销为35美元，但如何确定这条路径呢？

• 先找出钢琴的父节点【架子鼓】。
• 找到架子鼓的父节点【唱片】
• 找到唱片的父节点【乐谱】

所以最终路径是 乐谱 -> 唱片 -> 架子鼓 -> 钢琴

var graph = {
  yuepu: {
    changpain: 5,
    haibao: 0
  },
  haibao: {
    jita: 30,
    gu: 35,
  },
  changpain:{
    jita: 15,
    gu: 20
  },
  gu: {
    gangqing: 10
  },
  jita: {
    gangqing: 20
  },
  gangqing: {}
};
var costs = {
  changpain: 5,
  haibao: 0
}
var parents = {
  changpain: 'yuepu',
  haibao: 'yuepu',
};

// 问题二
// var graph = {
//   A: {
//     B: 5,
//     C: 2
//   },
//   B: {
//     D:4,
//     E:2
//   },
//   C:{
//     B: 8,
//     E: 7
//   },
//   D: {
//     F: 3,
//     E: 6
//   },
//   E: {
//     F:1
//   },
//   F: {}
// }
// var costs = {
//   B: 5,
//   C: 2
// }
// var parents = {
//   B: 'A',
//   C: 'A',
// };

var processed = [];
// 在未处理的节点中找出开销最小的节点
var node =  find_lowest_cost_node(costs); // haibao
while(node) {
  var cost = costs[node]; // 0
  var neighbors = graph[node];  // { jita: 30,gu: 35,}
  // 遍历当前节点的所有邻居
  for(var n in neighbors) {
    var new_cost = cost + neighbors[n]
    if(!costs[n]) {
      costs[n] = new_cost
      parents[n] = node   

    }
    // 如果经当前节点前往该邻居更近，
    if ( costs[n] > new_cost){
      // 就更新该邻居的开销
      costs[n] = new_cost
      // 同时将该邻居的父节点设置为当前节点
      parents[n] = node   
    }

  }
  // 将当前节点标记为处理过
  processed.push(node)
  // 找出接下来要处理的节点，并循环
  node = find_lowest_cost_node(costs)
}


console.log('graph', graph)
console.log('costs', costs)
console.log('parents', parents)
console.log('processed', processed)
function find_lowest_cost_node(costs) {
  let lowest_cost = Infinity 
  let lowest_cost_node = null 
  for (var node in costs) {
    var cost = costs[node] 
    if (cost < lowest_cost && !processed.includes(node)) {
      lowest_cost = cost
      lowest_cost_node = node 
    }
  }
  return lowest_cost_node
};

7.5实现

第八章 贪婪算法

本章内容

1.  学习如何处理不可能完成的任务：没有快速算法的问题（NP完全问题）。
2.  学习识别NP完全问题，以免浪费时间去寻找解决它们的快速算法。
3.  学习近似算法，使用它们可快速找到NP完全问题的近似解。
4.  学习贪婪策略——一种非常简单的问题解决策略。

8.1 教室调度问题

问题：假设有如下课程表，你希望将尽可能多的课程安排在某间教室上。你没法让这些课都在这间教室上，因为有些课的上课时间有冲突。

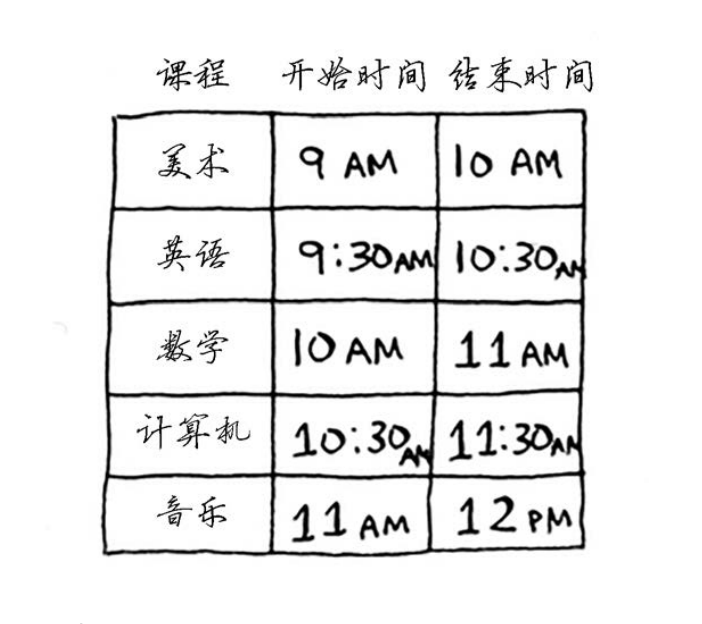
具体做法如下

1. 选出结束最早的课，它就是要在这间教室上的第一堂课。
2. 接下来，必须选择第一堂课结束后才开始的课。同样，你选择结束最早的课，这将是要 在这间教室上的第二堂课。

在这个示例中，每次都选择结束最早的课。用专业术语说，就是你每步都选择局部最优解，最终得到的就是全局最优解。

8.2 背包问题

问题： 假设你是个贪婪的小偷，背着可装4磅重东西的背包，在商场伺机盗窃各种可装入背包的商品。 其中 音响3000美元重4磅，笔记本2000美元重3磅，吉他1500美元重1磅。

具体做法如下：

1. 选择最贵的 音响3000美元
2. 选择第二贵的 最终只获得 3000元。但是如果选择 笔记本2000和吉他1500元，那么最终获得 3500元。

8.3 集合覆盖问题

8.4 NP 完全问题

8.5 小结

•  贪婪算法寻找局部最优解，企图以这种方式获得全局最优解。
•  对于NP完全问题，还没有找到快速解决方案。
•  面临NP完全问题时，最佳的做法是使用近似算法。
•  贪婪算法易于实现、运行速度快，是不错的近似算法。

第 九 章 动态规划

本章内容

•  学习动态规划，这是一种解决棘手问题的方法，它将问题分成小问题，并先着手解决这些小问题。
•  学习如何设计问题的动态规划解决方案。
• 动态规划算法的工作原理。动态规划先解决子问题，再逐步解决大问题。

9.1 背包问题

假设有个小偷，背着一个可装4磅东西的背包。可盗窃的商品有如下3件。音响3000美元重4磅，笔记本2000美元重3磅，吉他1500美元重1磅,iphone 2000美元重1磅 为了让盗窃的商品价值最高，该选择哪些商品？

-	1	2	3	4
小提琴	1500	1500	1500	1500
音响	1500	1500	1500	3000
笔记本	1500	1500	2000	3500
iphone	2000	3500, 放入了手机和吉他	3500, 放入了手机和吉他	4000， 放入笔记本和iphone

最优解可能导致背包

9.2.5 可以偷商品的一部分吗

TIP

假设你在杂货店行窃，可偷成袋的扁豆和大米，但如果整袋装不下，可打开包装，再将背包 倒满。在这种情况下，不再是要么偷要么不偷，而是可偷商品的一部分。如何使用动态规划来处 理这种情形呢？

答案是没法处理。使用动态规划时，要么考虑拿走整件商品，要么考虑不拿，而没法判断该 不该拿走商品的一部分。

但使用贪婪算法可轻松地处理这种情况！首先，尽可能多地拿价值最高的商品；如果拿光了， 再尽可能多地拿价值次高的商品，以此类推。

9.2.6 旅游行程最优化

假设你要去伦敦度假，假期2天，但你想去游览的地方很多。你没法前往每个地方游览，因 此你列个单子

对于想去游览的每个名胜，都列出所需的时间以及你有多想去看看。根据这个清单，你能确 定该去游览哪些名胜吗？

DANGER

但仅当每个子问题都是离散的，即不依赖于其他子问题时，动态规划才管用

练习

假设你要去野营。你有一个容量为6磅的背包，需要决定该携带下面的哪些东西。其中 每样东西都有相应的价值，价值越大意味着越重要：

•  水（重3磅，价值10）；
•  书（重1磅，价值3）  食物（重2磅，价值9）；
•  夹克（重2磅，价值5）；
•  相机（重1磅，价值6）。 请问携带哪些东西时价值最高？

9.3 最长公共子串（难点）

• 动态规划可帮助你在给定约束条件下找到最优解。在背包问题中，你必 须在背包容量给定的情况下，偷到价值最高的商品。
• 在问题可分解为彼此独立且离散的子问题时，就可使用动态规划来解决。 要设计出动态规划解决方案可能很难，这正是本节要介绍的。下面是一些通用的小贴士。
• 每种动态规划解决方案都涉及网格。
• 单元格中的值通常就是你要优化的值。在前面的背包问题中，单元格的值为商品的价值。
• 每个单元格都是一个子问题，因此你应考虑如何将问题分成子问题，这有助于你找出网 格的坐标轴。

9.3.4 最长公共子序列

• 生物学家根据最长公共序列来确定DNA链的相似性，进而判断度两种动物或疾病有多相 似。最长公共序列还被用来寻找多发性硬化症治疗方案。
• 你使用过诸如git diff等命令吗？它们指出两个文件的差异，也是使用动态规划实现的。
• 前面讨论了字符串的相似程度。编辑距离（levenshtein distance）指出了两个字符串的相 似程度，也是使用动态规划计算得到的。编辑距离算法的用途很多，从拼写检查到判断 用户上传的资料是否是盗版，都在其中。
• 你使用过诸如Microsoft Word等具有断字功能的应用程序吗？它们如何确定在什么地方断 字以确保行长一致呢？使用动态规划！

小结

• 需要在给定约束条件下优化某种指标时，动态规划很有用。
• 问题可分解为离散子问题时，可使用动态规划来解决。
• 每种动态规划解决方案都涉及网格。
• 单元格中的值通常就是你要优化的值。
• 每个单元格都是一个子问题，因此你需要考虑如何将问题分解为子问题。
• 没有放之四海皆准的计算动态规划解决方案的公式。

第 10 章 K最近邻算法 (k-nearest neighbours，KNN)

本章内容

• 学习使用K最近邻算法创建分类系统。
• 学习特征抽取。
• 学习回归，即预测数值，如明天的股价或用户对某部电影的喜欢程度。
• 学习K最近邻算法的应用案例和局限性。

10.1 橙子还是柚子

10.2 创建推荐系统

假设你是Netflix，要为用户创建一个电影推荐系统。 你可以将所有用户都放入一个图表中,这些用户在图表中的位置取决于其喜好，因此喜好相似的用户距离较近。 但还有一个重要的问题没有解决。，相似的用户相距较近，但如何确定两位用户的相似程度呢？

10.2.1 特征抽取

假设 橙子A的个头为 2，红的程度为2。柚子B的个头为2，红的程度为1。未知水果C 的个头为4，红的程度为4。 根据这些特征绘图。

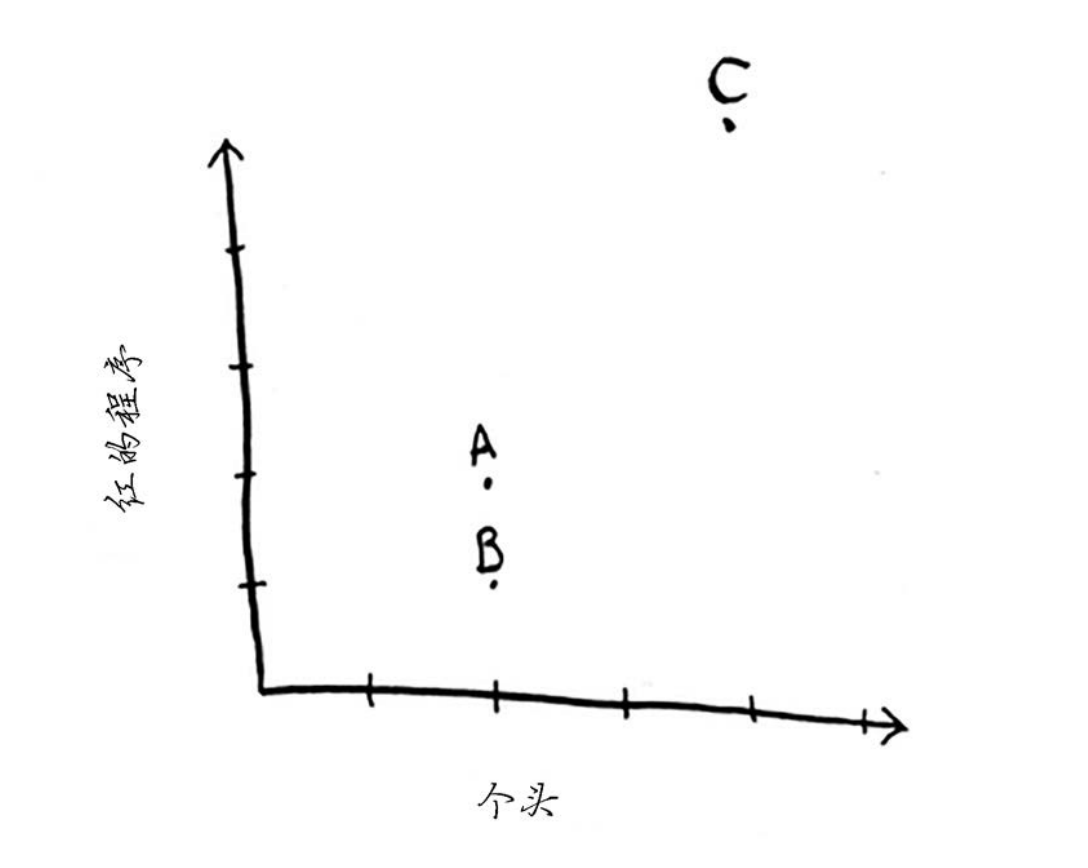
从上图可知，水果A和B比较像。下面来度量它们有多像。要计算两点的距离，可使用毕达哥拉斯公式。例如，A和B的距离如下。

五维空间中的距离

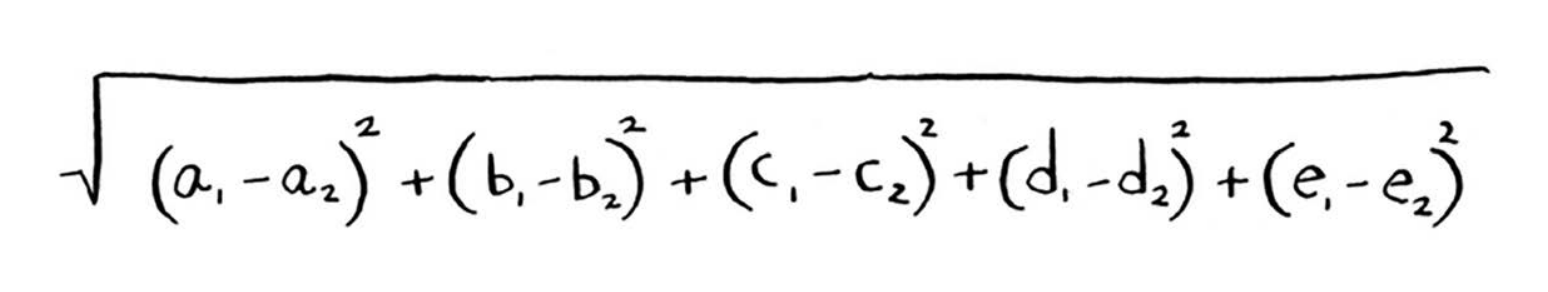
10.2.2 回归

假设你要预测Priyanka会给电影Pitch Perfect打多少分。Justin、JC、Joey、Lance和Chris都给 它分别打了 5，4，4，5，3分，

你求这些人打的分的平均值，结果为4.2。这就是回归（regression）。你将使用KNN来做两项 基本工作——分类和回归：

• 分类就是编组；
• 回归就是预测结果（如一个数字）

回归很有用。假设你在伯克利开个小小的面包店，每天都做新鲜面包，需要根据如下一组特 征预测当天该烤多少条面包：

• 天气指数1～5（1表示天气很糟，5表示天气非常好）；
• 是不是周末或节假日（周末或节假日为1，否则为0）；
• 有没有活动（1表示有，0表示没有）。

已有数据 A(5,1,0) = 300, B(3,1,1) = 225, C(1,1,0) = 75,D(4,0,1) = 200,E(4,0,0) = 150 F(2,0,0) = 50

今天是周末，天气不错,根据这些数据，预测你今天能售出多少条面包呢？我们来使用KNN 算法，其中的K为4。首先，找出与今天最接近的4个邻居。今天（4，1，0） = ？

距离如下

• 今天 - A 1
• 今天 - B 2
• 今天 - C 9
• 今天 - D 2
• 今天 - E 1
• 今天 - F 5

将A，B，D，E （300 + 225 + 200+150）/ 4 = 218.75 这些天售出的面包数平均，结果为218.75。这就是你今天要烤的面包数！

TIP

余弦相似度

前面计算两位用户的距离时，使用的都是距离公式。还有更合适的公式吗？在实际工作中， 经常使用余弦相似度（cosine similarity）。假设有两位品味类似的用户，但其中一位打分时更 保守。他们都很喜欢Manmohan Desai的电影Amar Akbar Anthony，但Paul给了5星，而Rowan只 给4星。如果你使用距离公式，这两位用户可能不是邻居，虽然他们的品味非常接近。

余弦相似度不计算两个矢量的距离，而比较它们的角度，因此更适合处理前面所说的情况。 本书不讨论余弦相似度，但如果你要使用KNN，就一定要研究研究它！

10.3 机器学习简介

KNN算法真的是很有用，堪称你进入神奇的机器学习领域的 领路人！机器学习旨在让计算机更聪明

10.3.1 OCR

OCR指的是光学字符识别（optical character recognition），这意味着你可拍摄印刷页面的照片， 计算机将自动识别出其中的文字

OCR的第一步是查看大量的数字图像并提取特征，这被称为训练（training）。大多数机器学 习算法都包含训练的步骤：要让计算机完成任务，必须先训练它

10.3.2 创建垃圾邮件过滤器

垃圾邮件过滤器使用一种简单算法——朴素贝叶斯分类器（Naive Bayes classifier），你首先 需要使用一些数据对这个分类器进行训练。

10.4 小结

•  KNN用于分类和回归，需要考虑最近的邻居。
•  分类就是编组。
•  回归就是预测结果（如数字）。
•  特征抽取意味着将物品（如水果或用户）转换为一系列可比较的数字。
•  能否挑选合适的特征事关KNN算法的成败。

第 11 章 10种算法

11.1 树

二叉查找树， 对于其中的每个节点，左子节点的值都比它小，而右子节点的值都比它大。

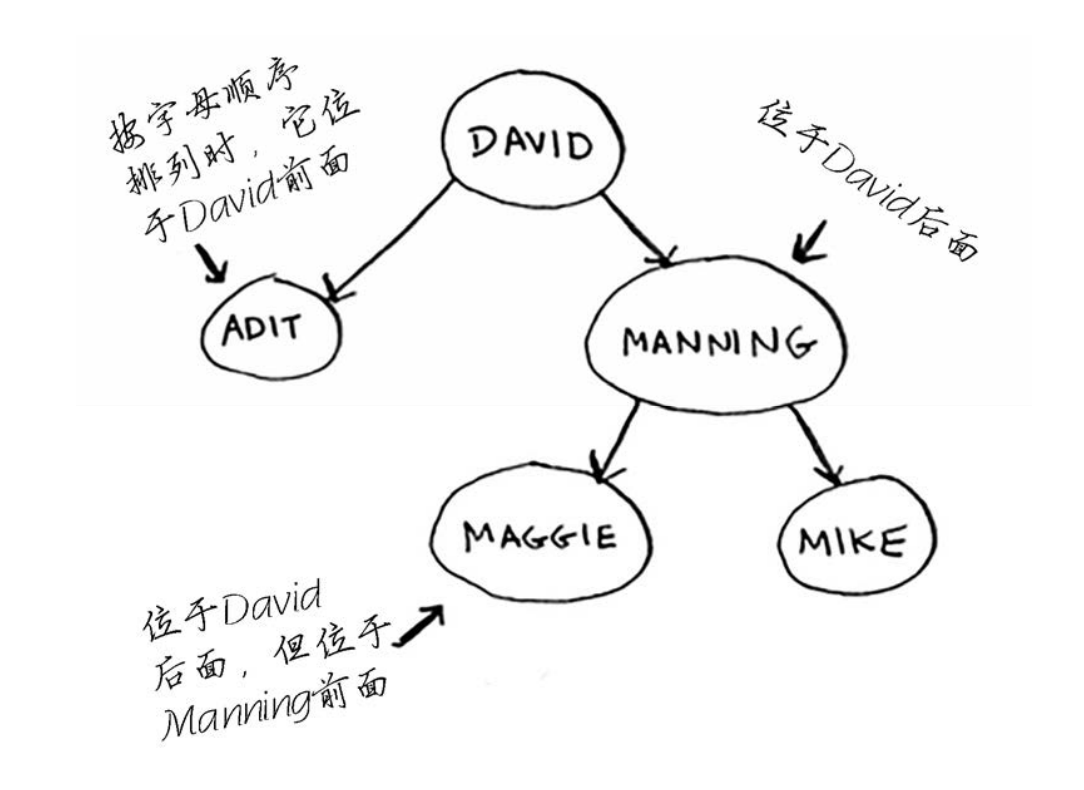
假设你要查找Maggie。为此，你首先检查根节点。Maggie排在David的后面，因此你往右边找。Maggie排在Manning前面，因此你往左边找。找到了。

TIP

在二叉查找树中查找节点时，平均运行时间为 O(log n)，但在最糟的情况下所需时间为O(n)；而在有序数组中查找时，即便是在最糟情况下所 需的时间也只有O(log n)，因此你可能认为有序数组比二叉查找树更佳。然而，二叉查找树的插 入和删除操作的速度要快得多。

不平衡的树，这棵树是向右倾斜的，因此性能不佳。也有一些处于平衡状态的特殊二叉查找树，如红黑树。

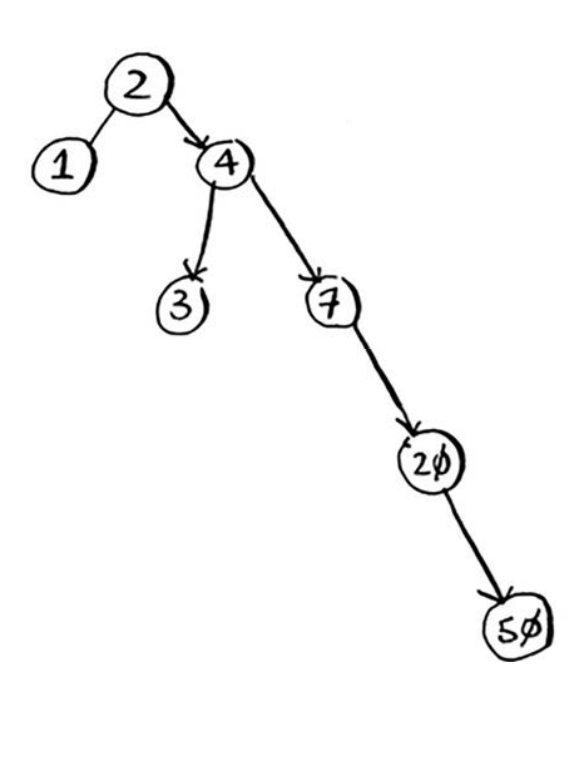
那在什么情况下使用二叉查找树呢？B树是一种特殊的二叉树，数据库常用它来存储数据。 如果你对数据库或高级数据结构感兴趣，请研究如下数据结构：B树，红黑树，堆，伸展树。

11.2 反向索引

这是一种很有用的数据结构：一个散列表，将单词映射到包含它的页面。这种数据结构被称为反向索引（inverted index），常用于创 建搜索引擎。

11.3 傅里叶变换

傅里叶变换算是一个绝妙、优雅且应用广泛的算法。

给定一首歌曲，傅里叶变换能够将其中的各种频率分离出来。

如果能够将歌曲分解为不同的频率，就可强化你关心的部分，如强化低音并隐藏高音。

傅里叶变换非常适合用于处理信号，可使用它来压缩音乐。为此，首先需要将音频文件分解为音符。傅里叶变换能够准确地指出各个音符对整个歌曲的 贡献，让你能够将不重要的音符删除。这就是MP3格式的工作原理！

数字信号并非只有音乐一种类型。JPG也是一种压缩格式，也采用了刚才说的工作原理。

傅里叶变换还被用来地震预测和DNA分析。

使用傅里叶变换可创建类似于Shazam这样的音乐识别软件。

11.4 并行算法

• 并行性管理开销。假设你要对一个包含1000个元素的数组进行排序，如何在两个内核之 间分配这项任务呢？如果让每个内核对其中500个元素进行排序，再将两个排好序的数组 合并成一个有序数组，那么合并也是需要时间的。

• 负载均衡。假设你需要完成10个任务，因此你给每个内核都分配5个任务。但分配给内核 A的任务都很容易，10秒钟就完成了，而分配给内核B的任务都很难，1分钟才完成。这意 味着有那么50秒，内核B在忙死忙活，而内核A却闲得很！你如何均匀地分配工作，让两 个内核都一样忙呢？

11.5 MapReduce 分布式算法

分布式算法非常适合用于在短时间内完成海量工作， MapReduce基于两个简单的理念：映射（map）函数和归并（reduce）函数。

11.5.2 映射函数

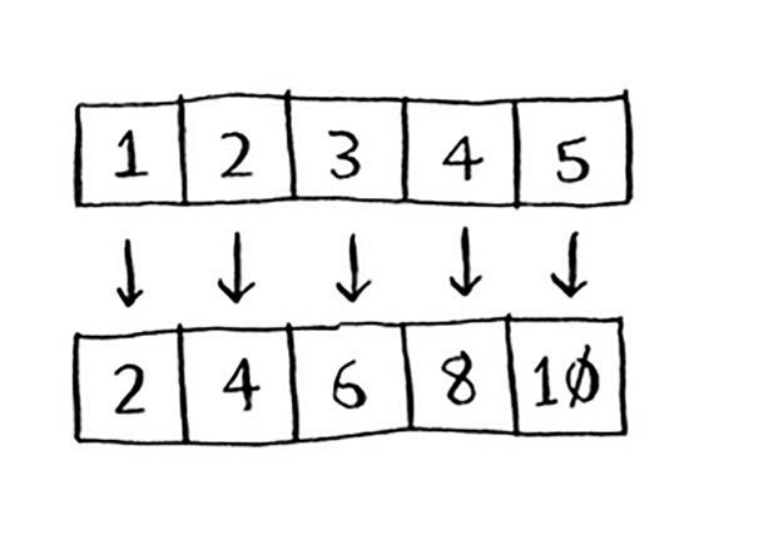
映射函数很简单，它接受一个数组，并对其中的每个元素执行同样的处理。例如，下面的映 射函数将数组的每个元素翻倍。

var arr = [1,2,3,4,5]
var arr2 = arr.map(item => item * 2)

11.5.3 归并函数

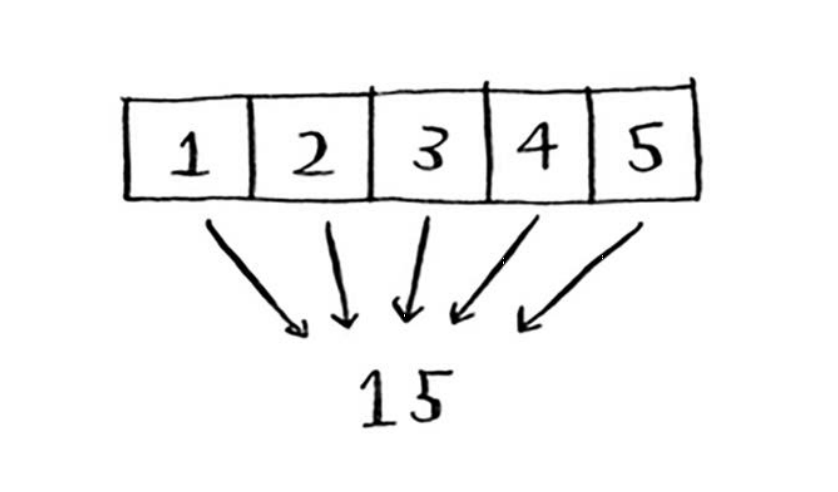
归并函数可能令人迷惑，其理念是将很多项归并为一项。映射是将一个数组转换为另一个数组。

var arr = [1,2,3,4,5]

var num = arr.reduce((total,value,currentIndex, d) => {

  return total + value
})

映射

归并

11.6 布隆过滤器和 HyperLogLog

布隆过滤器是一种概率型数据结构，它提供的答案有可能不对，但很可能是正确的。

HyperLogLog近似地计算集合中不同的元素数，与布隆过滤器一样，它不能给出准确的答案， 但也八九不离十，而占用的内存空间却少得多。

面临海量数据且只要求答案八九不离十时，可考虑使用概率型算法！

11.7 SHA 算法

安全散列算法（secure hash algorithm，SHA）函数。给定一个字符串，SHA返回其散列值。

SHA是一个散列函数，它生成一个散列值——一个较短的字符串。 用于创建散列表的散列函数根据字符串生成数组索引，而SHA根据字符串生成另一个字符串。 对于每个不同的字符串，SHA生成的散列值都不同。

你可使用SHA来判断两个文件是否相同，这在比较超大型文件时很有用。假设你有一个4 GB 的文件，并要检查朋友是否也有这个大型文件。为此，你不用通过电子邮件将这个大型文件发送 给朋友，而可计算它们的SHA散列值，再对结果进行比较。

SHA被广泛用于计算密码的散列值。这种散列算法是单向的。你可根据字符串计算出散列值。但你无法根据散列值推断出原始字符串。

SHA实际上是一系列算法：SHA-0、SHA-1、SHA-2和SHA-3。请使用SHA-2或SHA-3。 当前，最安全的密码散列函数是bcrypt，但没有任何东西是万无一失的。

11.8 局部敏感的散列算法

希望散列函数是局部敏感的。在这种情况下，可使用Simhash。 如果你对字符串做细微的修改，Simhash生成的散列值也只存在细微的差别。这让你能够通过比 较散列值来判断两个字符串的相似程度，这很有用！

• Google使用Simhash来判断网页是否已搜集。
• 老师可以使用Simhash来判断学生的论文是否是从网上抄的。
• Scribd允许用户上传文档或图书，以便与人分享，但不希望用户上传有版权的内容！这个 网站可使用Simhash来检查上传的内容是否与小说《哈利·波特》类似，如果类似，就自动拒绝。
• 需要检查两项内容的相似程度时，Simhash很有用。

11.9 Diffie-Hellman 密钥交换

• 双方无需知道加密算法。

Diffie-Hellman使用两个密钥：公钥和私钥。顾名思义，公钥就是公开的，可将其发布到网站 上，通过电子邮件发送给朋友，或使用其他任何方式来发布。你不必将它藏着掖着。有人要向你 发送消息时，他使用公钥对其进行加密。加密后的消息只有使用私钥才能解密。只要只有你知道 私钥，就只有你才能解密消息！

Diffie-Hellman算法及其替代者RSA依然被广泛使用。

11.10 线性规划

线性规划用于在给定约束条件下最大限度地改善指定的指标。例如，假设你所在的公司生产 两种产品：衬衫和手提袋。衬衫每件利润2美元，需要消耗1米布料和5粒扣子；手提袋每个利润3 美元，需要消耗2米布料和2粒扣子。你有11米布料和20粒扣子，为最大限度地提高利润，该生产 多少件衬衫、多少个手提袋呢？

目标是利润最大化，而约束条件是拥有的原材料数量。

所有的图算法都可使用线性规划来实现。线性规划是一个宽泛得多的框架，图问题只是其中的一个子集。

线性规划使用Simplex算法，这个算法很复杂