# 啊哈-算法
# 第一章 一大波数正在靠近——排序
# 第 1 节 最快最简单的排序——桶排序
假如现在有 5个人,总分10分。每人的得分分别是 5 3 5 2 8。请你为这5个人按从小到大的顺序排序,我们就可以用简化版桶排序(不是真正的桶排序)实现。
时间复杂度 O(M + N),m 为桶的个数,n 为待排序数的个数
优点:
速度快 缺点:
浪费空间
我们要表示0-10分,所以需要11个桶
var book = Array.from({length: 11}).fill(0);
var score = [5, 3, 5, 2, 8];
for (var i =0, len = score.length; i < len; i++) {
book[score[i]] ++
}
for (var j = 0,len = book.length; j <len; j++) {
for(var k = 0; k < book[j]; k++) {
console.log('得分', j)
}
}
console.log(book)
2
3
4
5
6
7
8
9
10
11
12
13
14
15
# 第 2 节 邻居好说话——冒泡排序
冒泡排序的基本思想是:每次比较两个相邻的元素,如果它们的顺序错误就把它们交换过来。
时间复杂度 O(n ^ 2)
优点: 空间占用小 缺点: 用时长
var arr = [8, 100, 50, 22, 15, 6, 1, 1000, 999, 0, 10,10 ,10]
for(var i = 0; i < arr.length - 1; i++) { // 因为 循环完 arr.length - i后,最后一个肯定被排序了
for(var j = 0; j< arr.length - i - 1; j++) { // 大循环一次就有一个被找到,所以是 arr.length - i
if(arr[j] < arr[j + 1]) {
var max = arr[j]
arr[j] = arr[j+1]
arr[j + 1] = max
}
}
}
2
3
4
5
6
7
8
9
10
解决:现在分别有 5 个人的名字和分数:huhu 5 分、haha 3 分、xixi 5 分、hengheng 2 分和 gaoshou 8 分。
var arr = [{name: 'huhu',score: 5},{name: 'haha',score: 3},{name: 'xixi',score: 5},{
name: 'hengheng ',score: 2},{name: 'gaoshou',score: 8}]
for(var i = 0; i < arr.length - 1; i++) {
for(var j = 0; j< arr.length - i - 1; j++) {
if(arr[j].score < arr[j + 1].score) {
var max = arr[j]
arr[j] = arr[j+1]
arr[j + 1] = max
}
}
}
2
3
4
5
6
7
8
9
10
11
12
# 第 3 节 最常用的排序——快速排序
假设我们现在对“6 1 2 7 9 3 4 5 10 8”这 10 个数进行排序。
var arr = [6, 1, 2, 7, 9, 3, 4, 5, 10, 8]
function quicksort(left, right) {
if(left > right) {
return
}
var temp = arr[left] // 6
var i = left // 0 3
var j = right // 7
while(i!=j) {
while(arr[j] >= temp && i < j) {
j --
}
while(arr[i] <= temp && i < j) {
i ++
}
if(i < j) {
t = arr[i]
arr[i] = arr[j]
arr[j] = t
}
}
arr[left]= arr[i];
arr[i]=temp;
quicksort(left,i-1);//继续处理左边的,这里是一个递归的过程
quicksort(i+1,right);
}
quicksort(0, arr.length - 1)
console.log('arr======', arr)
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
# 第 4 节 小哼买书
问题一:表示有 n 个同学参与调查(n≤100),每个同学可以选择一本自己喜欢的书,并计书的ISBN 号为 1~1000之间,并将ISBN号排序,要求1秒计算出
桶排序
冒泡排序
快速排序
三种方式
2
3
4
问题二:表示有 n 个同学参与调查(n≤100),每个同学可以选择一本自己喜欢的书,并计书的ISBN 号为 -2147483648~2147483647之间,要求1秒计算出 不能用桶排序,因为内存空间占用太多
问题三:表示有 n 个同学参与调查(n≤1000000),每个同学可以选择一本自己喜欢的书,并计书的ISBN 号为 1~1000之间,要求1秒计算出 不用冒泡排序,因为时间复杂度是 O(1000000 * 1000000)需要10秒,超时了。
可以用快速排序,时间为 100000×log2100000≈100000×17≈170 万次
我们来回顾一下本章三种排序算法的时间复杂度。桶排序是最快的,它的时间复杂度是O(N+M);冒泡排序是 O(N^2);快速排序是 O(NlogN)。
# 第二章 栈、队列、链表
# 参考
链表+6道前端算法面试高频题解 (opens new window)
# 第 1 节 解密 QQ 号——队列
女神的QQ6 3 1 7 5 8 9 2 4可以如下解密方式
规则是这样的:首先将第 1 个数删除,紧接着将第 2 个数放到 这串数的末尾,再将第 3 个数删除并将第 4 个数放到这串数的末尾,再将第 5 个数删除…… 直到剩下最后一个数,将最后一个数也删除。按照刚才删除的顺序,把这些删除的数连在一 起就是她的 QQ 啦。
方式一
var arr = [6, 3, 1, 7, 5, 8, 9, 2, 4]
var target =[]
while(arr.length) {
target.push(arr.shift())
arr.length && arr.push(arr.shift())
}
console.log('target', target)
方式二
var arr = [,6, 3, 1, 7, 5, 8, 9, 2, 4]
var target =[]
var head = 1
var tail = arr.length
while( head < tail) {
// 打印队首并将队首出队
target.push(arr[head])
console.log('object', arr[head])
head ++
// /先将新队首的数添加到队尾
arr[tail] = arr[head]
tail++
//再将队首出队
head ++
}
console.log('target', target)
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
# 第 2 节 解密回文——栈
请判断下列数据是不是回文,回文肯定是基数。 ahaha, aha,ahah,xyzyx
解法一
var isPalindrome = function(s) {
var str = s.toLocaleLowerCase().replace(/[^\da-zA-Z]/g,'')
var len =str.length
var mid = parseInt(len / 2) - 1
var prev = []
var top = 0
var next = 0
for (var i =0; i <= mid ;i++) {
prev[++top] = str[i]
}
if (len % 2 == 0) {
next = mid + 1
} else {
next = mid + 2
}
for(var j = next; j < len;j++){
if(str[j] != prev[top]){
break;
}
top --
}
if(top === 0) {
return true
}
return false
};
解法二
var isPalindrome = function(s) {
var strArr = s.toLocaleLowerCase().replace(/[^\da-zA-Z]/g,'')
var reverse = strArr.split('').reverse().join('')
return strArr === reverse
};
解法三
var isPalindrome = function(s) {
var strArr = s.toLocaleLowerCase().replace(/[^\da-zA-Z]/g,'')
var start = 0
var end = strArr.length - 1
var is = true
while(start < end) {
if(strArr[start] !== strArr[end]) {
is = false
break;
}
start ++
end --
}
return is
};
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
# 第 3 节 纸牌游戏——小猫钓鱼
将一副扑克牌平均分成两份,每人拿一份。小哼先拿出手中的 第一张扑克牌放在桌上,然后小哈也拿出手中的第一张扑克牌,并放在小哼刚打出的扑克牌 的上面,就像这样两人交替出牌。出牌时,如果某人打出的牌与桌上某张牌的牌面相同,即 可将两张相同的牌及其中间所夹的牌全部取走,并依次放到自己手中牌的末尾。当任意一人 手中的牌全部出完时,游戏结束,对手获胜。
小哼手中有 6 张牌,顺序为 2 4 1 2 5 6,小哈手中也有 6 张牌,顺序为 3 1 3 5 6 4,最终谁会获胜呢?
# 第 4 节 链表
# 第 5 节 模拟链表
我们可以用一个数组 data 来存储每序列中的每一个数。
再用一个数组right来存放序列中每一个数右边的数.
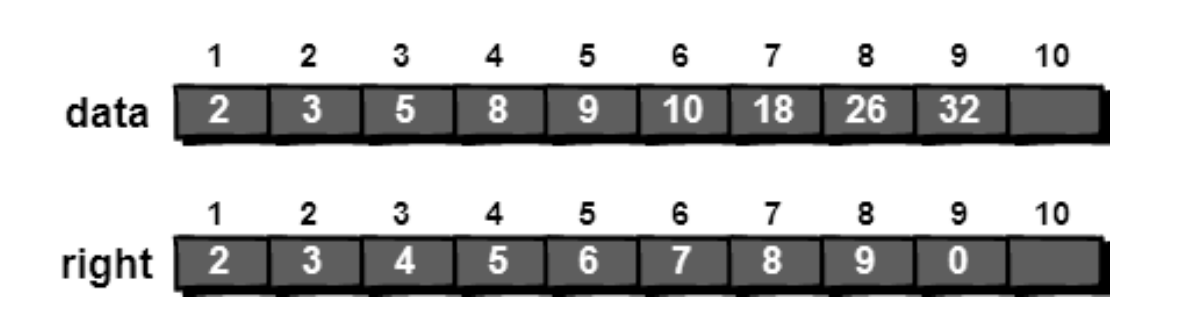
第一个整型数组 data 是用来存放序列中具体数字的,
另外一个整型数组 right 是用来存放当前序列中每一个元素右边的元素在数组 data 中位置的。
例如 right[1]的值为 2,就表示当前序列中 1 号元素右边的元素存放在 data[2]中;如果是 0,例如 right[9] 的值为 0,就表示当前序列中 9 号元素的右边没有元素。
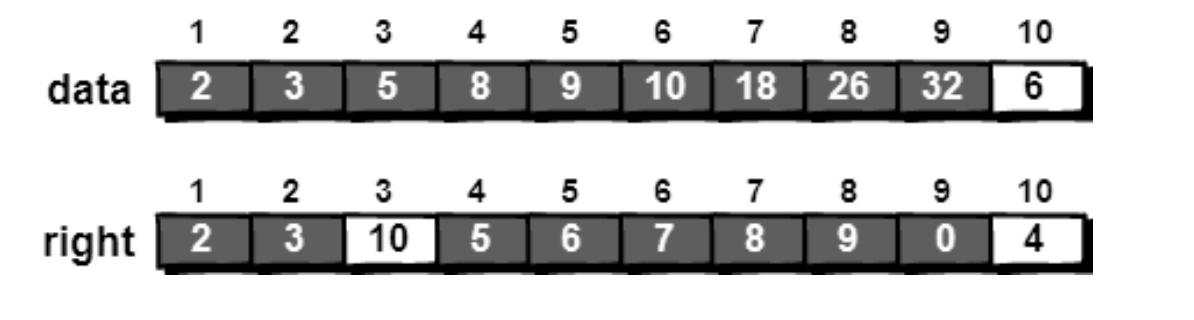
现在需要在 8 前面插入一个 6,只需将 6 直接存放在数组 data 的末尾即 data[10]=6。接下 来只需要将right[3]改为10,表示新序列中3号元素右边的元素存放在data[10]中。再将right[10] 改为 4,表示新序列中 10 号元素右边的元素存放在 data[4]中。这样我们通过 right 数组就可以 从头到尾遍历整个序列了(序列的每个元素的值存放在对应的数组 data 中).
# 第三章 枚举 很暴力
# 第 1 节 坑爹的奥数
有如下题目,[]3 * 6528 = 3[]*8256, 在括号中填入相同的数字使得等式成立
for(var i = 0 ;i < 10;i++) {
if((i * 10 + 3) * 6528 === (3 * 10 + i) * 8256){
console.log(i)
break
}
}
2
3
4
5
6
[][][] + [][][] = [][][], 将数字1~9分别填入9个[]中,每个数字只能使用一次使得等式成立。例如 173 + 286 = 459。 请问有多少种组合。173 + 286 和 286 + 173 是一个组合。
var book = [];
var a = [];
var total = 0
for(a[1] = 1; a[1] < 10; a[1]++) {
for(a[2] = 1; a[2] < 10; a[2]++) {
for(a[3] = 1; a[3] < 10; a[3]++) {
for(a[4] = 1; a[4] < 10; a[4]++) {
for(a[5] = 1; a[5] < 10; a[5]++) {
for(a[6] = 1; a[6] < 10; a[6]++) {
for(a[7] = 1; a[7] < 10; a[7]++) {
for(a[8] = 1; a[8] < 10; a[8]++) {
for(a[9] = 1; a[9] < 10; a[9]++) {
book = [] // 每次都清空
for(var i = 1; i < 10; i++ ) {
book[a[i]] = 1 // 出现过的数字就设置为 1 ,有可能 a[1] 也是5, a[2]也是5
}
var sum = book.reduce((total,item) =>{
return total + item
}) // 看看是不是出现了9个不同的数
if(sum === 9 && a[1] * 100 + a[2] * 10 + a[3] + a[4] * 100 + a[5] * 10 + a[6] === a[7] * 100 + a[8] * 10 + a[9]){
console.log('object', a[1],a[2],a[3],a[4], a[5],a[6] ,a[7],a[8],a[9])
total ++
}
}
}
}
}
}
}
}
}
}
console.log('组合', total /2)
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
# 第 2 节 炸弹人
小霸王炸弹人
假如只有一枚炸弹,炸弹可消灭范范围内所有敌人。炸弹放哪里最好呢?

# 第 3 节 火柴棍等式
假如你有N根火柴棍,希望拼出 形如 A+B=C 的等式,等式中的A,B,C均是用火柴拼出来的整数(若该数非零,则最高位不能是0),0-9如下图

例如 你有14根火柴,则可以拼出 0 + 1 = 1,1 + 0 = 1
- 加号与等于号各自需要两根火柴
- 如果 A 不等于B,则 A+B=C 与B+A=C视为不同的等式,(A,B,C)都大于0
- 所有火柴必须全用
假如你有24根火柴,有多少拼法。
# 第 4 节 数的全排列
求 123的全排序,求 123456789的全排列
# 第四章 万能的搜索
# 第 1 节 深度优先搜索
有1,2,3三张牌,分别放到3个盒子里,有多少放法。
var book = [];
var a = [];
var n = 3;
function dfs(step){
var i
if(step == n + 1) {
console.log(a)
return
}
for (i = 1; i < n + 1; i++) {
if(!book[i]) {
a[step] = i
book[i] = 1
dfs(step + 1)
book[i] = 0
}
}
return
}
// dfs(1)
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
# 第 2 节 解救小哈
小哈进入迷宫,找不到出口。小哼从入口 1,1出发去寻找 处于4,3位置的小哈。
0代表可以通行,1代表不可通行,找出最短路径
var n = 5,m = 4,p = 4,q = 3,min = 99999999
var a = [
[0,0,1,0],
[0,0,0,0],
[0,0,1,0],
[0,1,0,0],
[0,0,0,1]
]
var book = [[],[,1],[],[],[]]
var next = [[0,1], [1,0], [0, -1], [-1,0]]
function dfs(x, y , step) {
console.log('step', step)
// 右 下 左 上
var tx, ty, k;
// 上下左右四种走法
for (var k = 0; k < 4; k++) {
// 下一个点的位置
tx = x + next[k][0];
ty = y + next[k][1];
// 判断是否越界
if (tx < 0 || tx > n - 1 || ty < 0 || ty > m - 1) {
continue
}
// 找到了目标位置
if(tx == p && ty == q) {
if(step < min) {
// 更新最新值
min = step
}
return
}
// 判断该点是否是障碍物或者 已经走过了
if(a[tx][ty] == 0 && !book[tx][ty]){
book[tx][ty] = 1 // 标记该点已经走过了
dfs(tx, ty, step + 1); // 走下一个点
book[tx][ty] = 0 // 尝试结束,取消这个点的标记
}
}
return
}
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
# 第 3 节 层层递进-广度优先搜索
广度优先搜索解救小哈
var point = [];
var book = [];
var min = 99999
var head = 0
var tail = 0
var queue = []
var next = [[0,1],[1,0],[0,-1],[-1,0]]
var x,y,f,s // 横坐标,纵坐标,父亲在队列的编号,步数
var i,j,k,n,m,startx,starty,p,q,tx,ty,flag
function mian(params) {
queue[tail] = {}
queue[tail].x = startx
queue[tail].y = starty
queue[tail].f = 0
queue[tail].s = 0
}
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
# 第 4 节 再解炸弹人
# 第 5 节 宝岛探险
# 第 6 节 水管工游戏
# 第五章 图的遍历
# 第 1 节 深度和广度优先究竟是啥
针对图的遍历方式
图就是由顶点和边组成的。
深度遍历是递归查找的过程
广度遍历是栈遍历的过程
如何储存一个图?
最常用的方法是使用二维数组
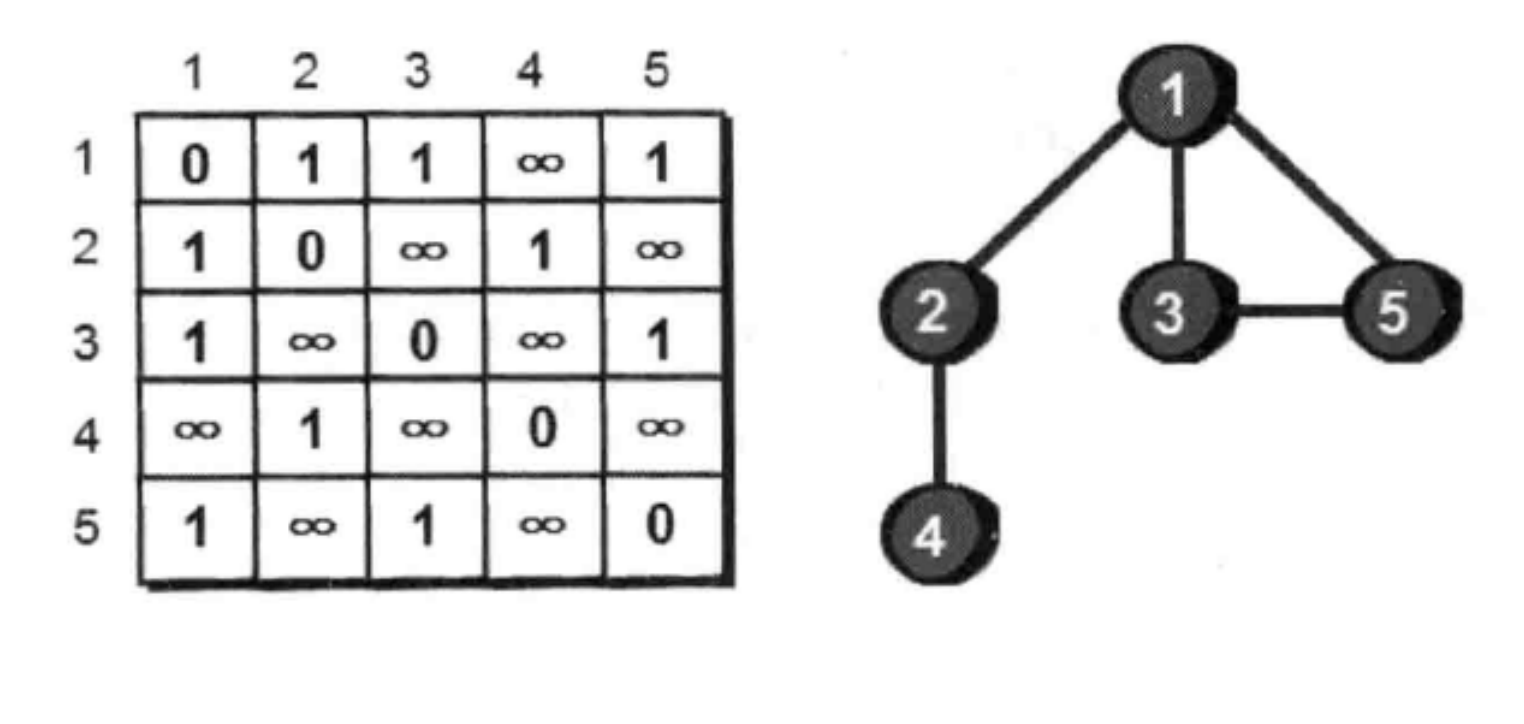
上图二维数组中第i行第j列表示的是顶点i到顶点j是否右边,1表示有,∞表示没有,0表示自己到自己。 我们将这种储存图的方法称为图的邻接矩阵存储法
使用深度优先搜索和广度优先搜索来遍历图都会得到这个图的生成树。
# 第 2 节 城市地图-图的深度优先遍历
求最短路径可以使用 深度优先,广度优先,Floyd, Bellman-ford ,Dijkstra
# 第 3 节 最少转机 - 图的广度优先遍历
# 第六章 最短路径
# 第 1 节 只有五行的算法,Floyd-Warshall
# 第 2 节 Dijkstra算法, 通过边实现松弛
# 第 3 节 Bellman-Ford - 解决负权边
# 第 4 节 Bellman-Ford的队列优化
# 第七章 神奇的树
# 第 1 节 开启树之旅
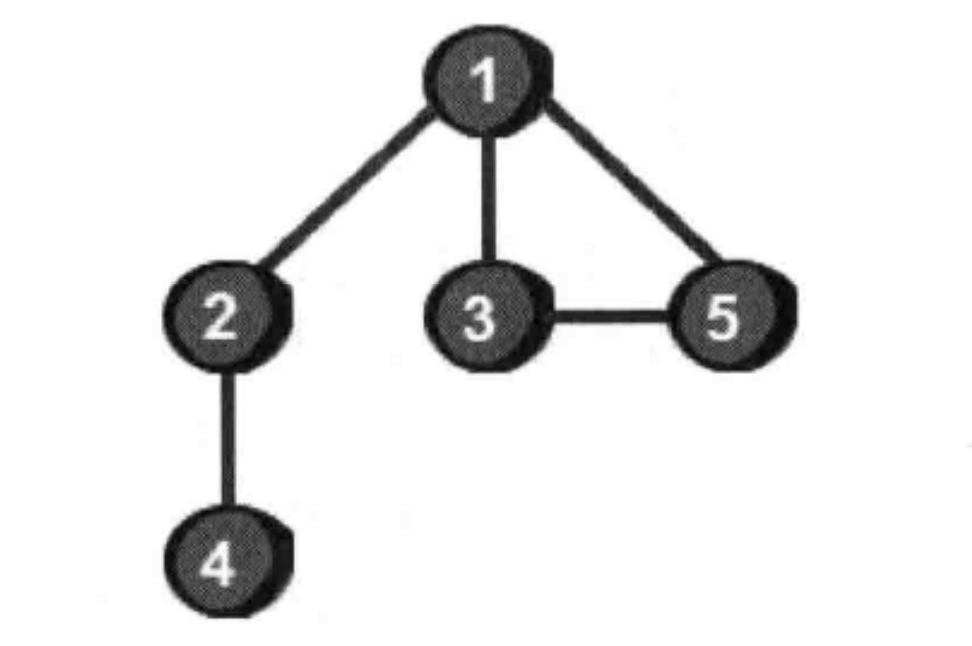
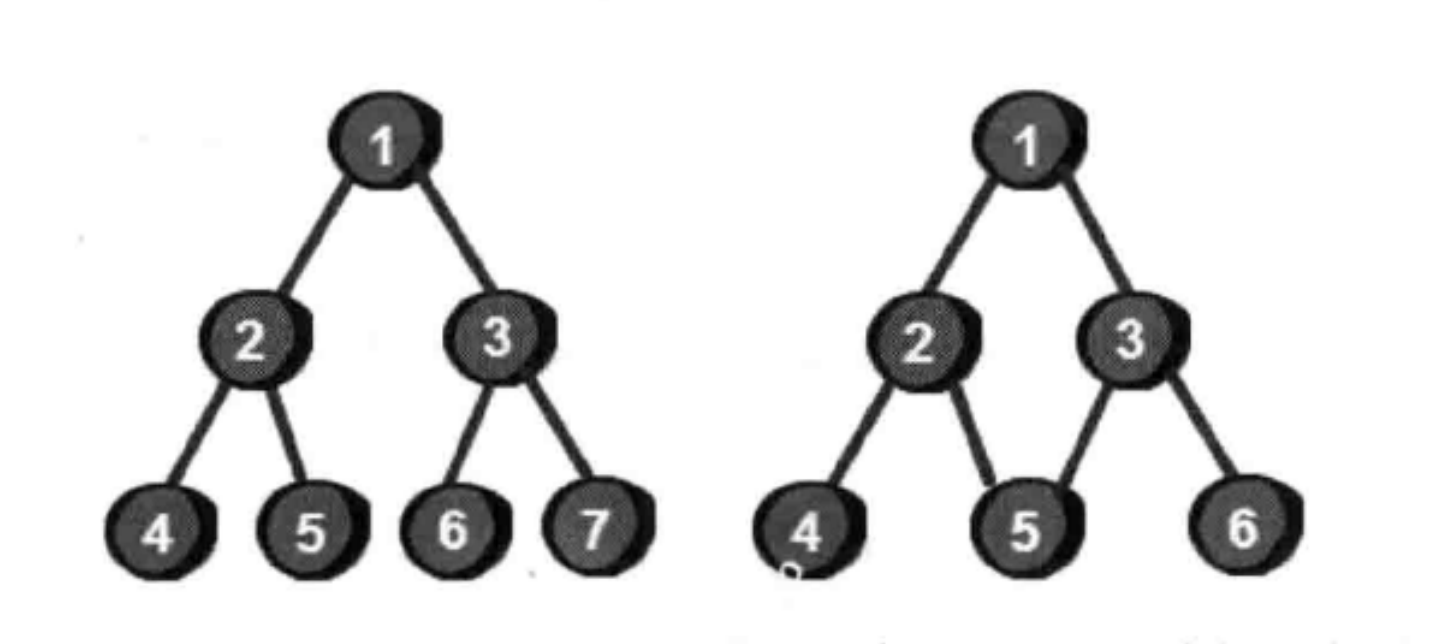
树其实是不包含回路的连通无向图。
树是指任意两个节点间有且只有一条路径的无向图。
左边是树,右边是图
右边的图,可以形成 1->2->5->3->1,左边的树不可以
树有以下特点
- 一颗树种的任意两点有且仅有唯一的一条路径连通
- 一棵树如果有n 个节点,那么它恰好有n-1条边
- 在一颗树种加入一条边会构成一个回路
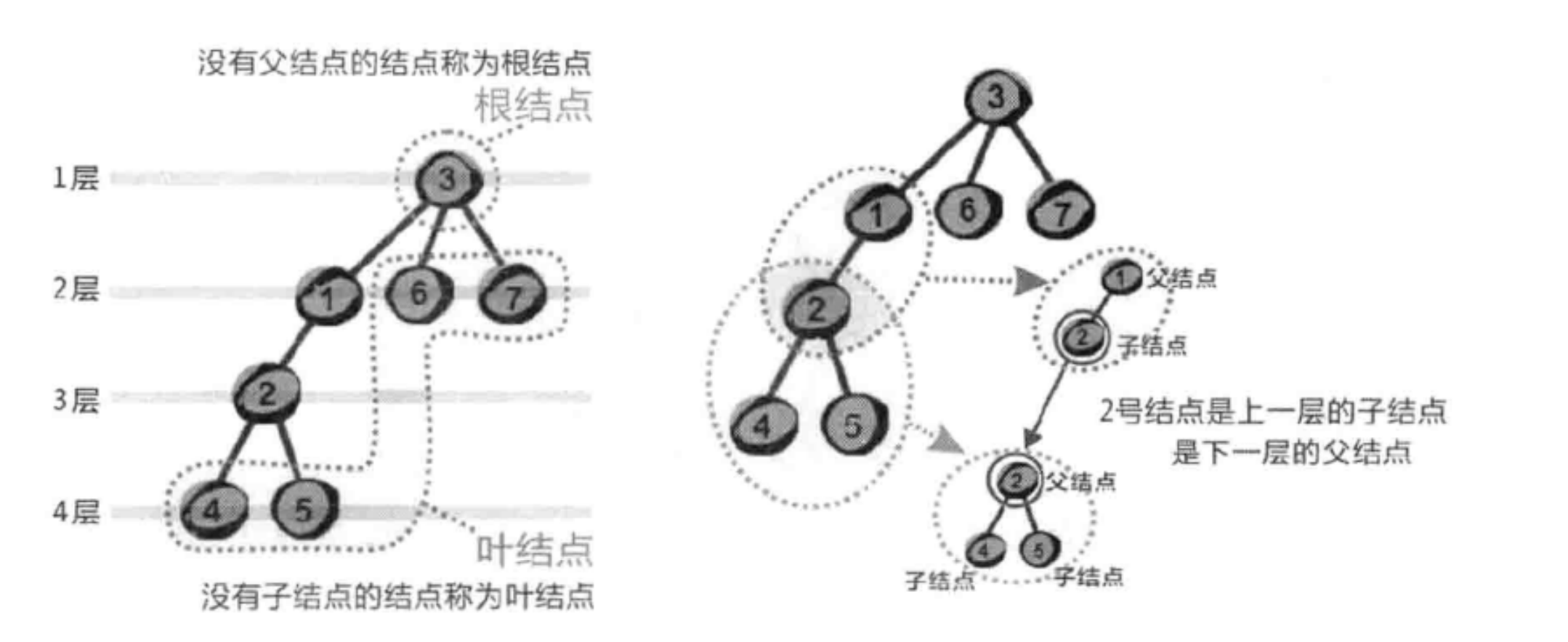
树的术语
根节点,子节点,叶节点
# 第 2 节 二叉树
二叉树是一种特殊的树,每个节点只有最多有两个子节点。
二叉树要么为空,要么由根节点,左子树 和右子树组成。而左子树和右子树分别是一颗二叉树。
二叉树中还有两颗特殊的树,叫做满二叉树和完全二叉树。
如果二叉树中每个内部节点都有两个儿子,这样的树称为满二叉树。严格定义是 深度为h 且有2^n - 1个节点的二叉树
设二叉树的高度为h, 除第h层外,其他各层(1~h-1)的节点数都达到最大个数,第h层从右向左连续缺若干节点,则这个二叉树就是完全二叉树。
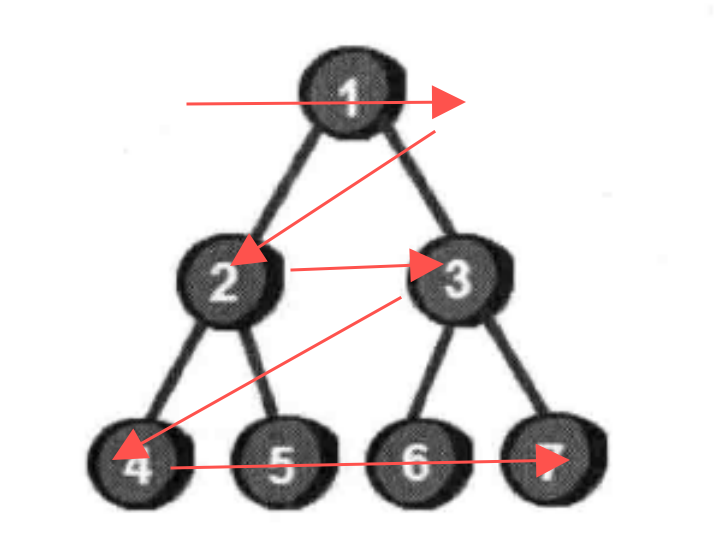
通过上图,我们发现如果完全二叉树的一个父节点编号为k,那么它左边儿子的编号就是2*k,右边儿子的编号就是2*k+ 1
如果一颗完全二叉树有N个节点,那么它的高度就是 log2N,简写为logN。
# 第 3 接 堆 - 神奇的优先队列
堆是特殊的完全二叉树
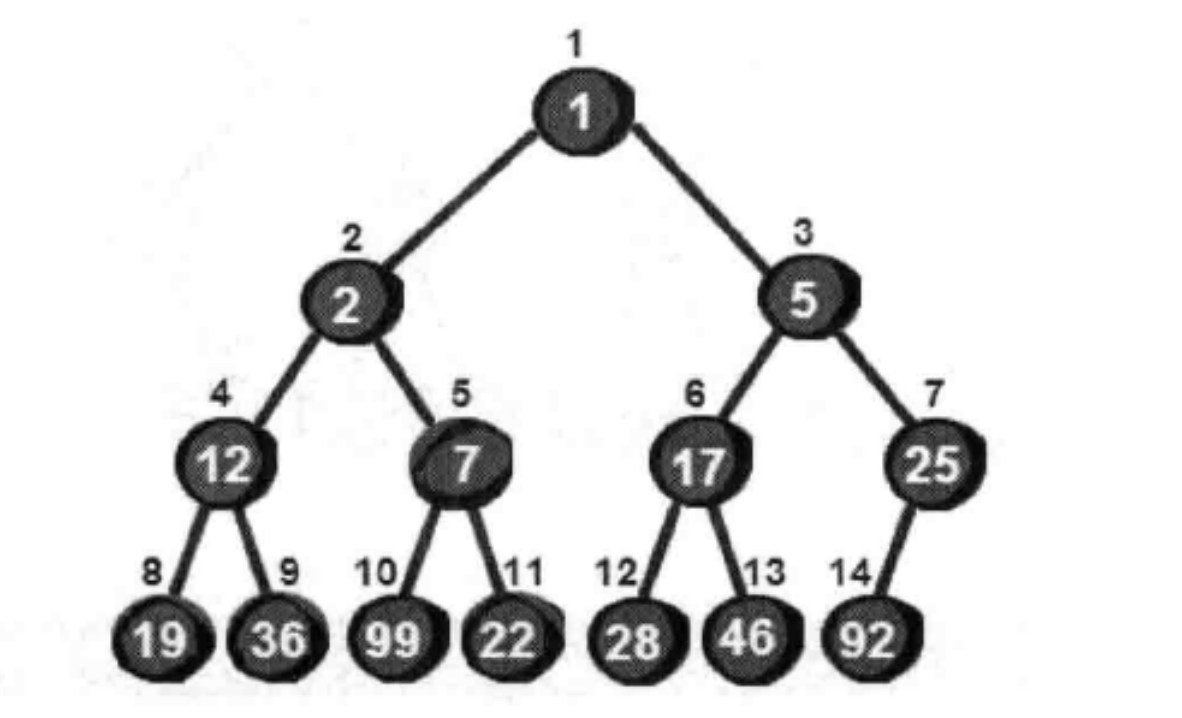
所有父节点比子节点小的完成二叉树称为最小堆,所有父节点比子节点大的完成二叉树称为最大堆。
堆排序
像这样支持插入元素和寻找最大(小)值元素的数据结构称为优先队列。
# 第 4 节 擒贼先擒王- 并查集
并查集也称为不相交集数据结构。
# 小结
线段树,树状数组,字典树,二叉搜索树,红黑树(平衡二叉搜索树)